大家好、今天我们一起学习探索性分析,主要有以下几个目的:
1、对数据进行过滤和检查,识别离群值、极值、数据中的缺口等其他特征;验证数据的分布特征,正态分布、方差齐性或者不齐性;对不满足的数据,提示转换方法;
2、描述统计量,通过输出直方图、茎叶图、箱体图,来描述个案、各组之间的特征。话不多说,直接上操纵。
原始数据
研究问题:探究男女薪水之间的关系
操作:分析→描述统计→探索
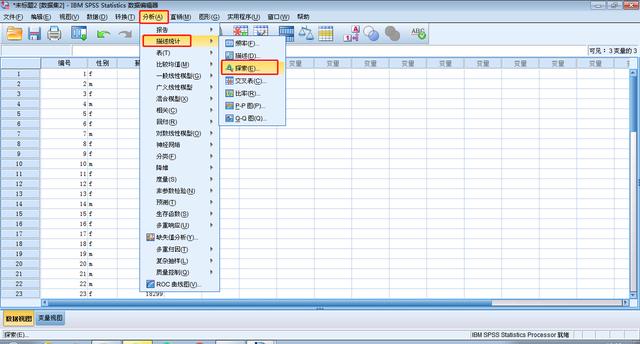
探索性分析
统计量:
描述性:均值,方差等,均值置信区间可以自己调整
M-估计量:四种权重项的最大似然数,样本平均数、中位数稳健的替代值,用于估计位置
界外值:输出五个最大值和五个最小值
百分位数:输出第5%、10%、15%、25%……95%位置的值
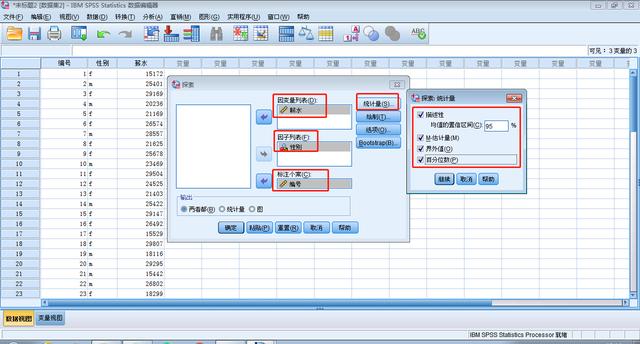
统计量
绘制
茎叶图、直方图、带检验的正态图、未转换
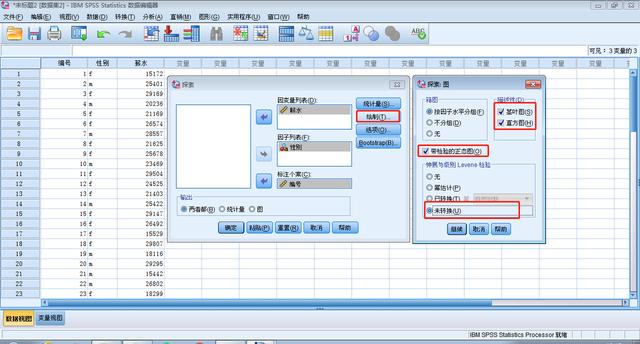
绘制
确定→输出结果
案例处理摘要 | |||||||
性别 | 案例 | ||||||
有效 | 缺失 | 合计 | |||||
N | 百分比 | N | 百分比 | N | 百分比 | ||
薪水 | 女 | 26 | 100.0% | 0 | 0.0% | 26 | 100.0% |
男 | 22 | 100.0% | 0 | 0.0% | 22 | 100.0% | |
男性有22个案例,女性有26个案例,缺失值无。
描述 | |||||
性别 | 统计量 | 标准误 | |||
薪水 | 女 | 均值 | 23072.38 | 881.637 | |
均值的 95% 置信区间 | 下限 | 21256.62 | |||
上限 | 24888.15 | ||||
5% 修整均值 | 23146.59 | ||||
中值 | 22844.50 | ||||
方差 | 20209389.526 | ||||
标准差 | 4495.485 | ||||
极小值 | 15042 | ||||
极大值 | 29807 | ||||
范围 | 14765 | ||||
四分位距 | 6284 | ||||
偏度 | -.180 | .456 | |||
峰度 | -.834 | .887 | |||
男 | 均值 | 23424.45 | 971.636 | ||
均值的 95% 置信区间 | 下限 | 21403.83 | |||
上限 | 25445.08 | ||||
5% 修整均值 | 23520.47 | ||||
中值 | 25033.50 | ||||
方差 | 20769675.688 | ||||
标准差 | 4557.376 | ||||
极小值 | 15442 | ||||
极大值 | 29626 | ||||
范围 | 14184 | ||||
四分位距 | 8212 | ||||
偏度 | -.406 | .491 | |||
峰度 | -1.300 | .953 | |||
描述性统计量,其中5% 修整均值是指截去5%以后的数据求的平均值。
M-估计器 | |||||
性别 | Huber 的 M-估计器a | Tukey 的双权重b | Hampel 的 M-估计器c | Andrews 波d | |
薪水 | 女 | 23147.46 | 23224.09 | 23163.74 | 23221.36 |
男 | 24023.32 | 24006.01 | 23713.92 | 24002.15 | |
a. 加权常量为 1.339。 | |||||
b. 加权常量为 4.685。 | |||||
c. 加权常量为 1.700、3.400 和 8.500 | |||||
d. 加权常量为 1.340*pi。 | |||||
M估计值与均值有一定的差异,说明数据中存在异常值,不是很明显的正态分布。
百分位数 | |||||||||
性别 | 百分位数 | ||||||||
5 | 10 | 25 | 50 | 75 | 90 | 95 | |||
加权平均(定义 1) | 薪水 | 女 | 15087.50 | 15421.90 | 20228.25 | 22844.50 | 26512.50 | 29269.50 | 29700.95 |
男 | 15578.35 | 16546.60 | 18795.25 | 25033.50 | 27007.00 | 29073.60 | 29576.35 | ||
Tukey 的枢纽 | 薪水 | 女 | 20323.00 | 22844.50 | 26492.00 | ||||
男 | 18925.00 | 25033.50 | 26836.00 | ||||||
女性第5%位置上的薪水为15087.50,等等,以此类推。
极值 | ||||||
性别 | 案例号 | 编号 | 值 | |||
薪水 | 女 | 最高 | 1 | 18 | 18 | 29807 |
2 | 11 | 11 | 29504 | |||
3 | 3 | 3 | 29169 | |||
4 | 15 | 15 | 29147 | |||
5 | 35 | 35 | 28955 | |||
最低 | 1 | 27 | 27 | 15042 | ||
2 | 1 | 1 | 15172 | |||
3 | 17 | 17 | 15529 | |||
4 | 23 | 23 | 18299 | |||
5 | 38 | 38 | 18488 | |||
男 | 最高 | 1 | 28 | 28 | 29626 | |
2 | 20 | 20 | 29295 | |||
3 | 7 | 7 | 28557 | |||
4 | 39 | 39 | 27694 | |||
5 | 29 | 29 | 27520 | |||
最低 | 1 | 21 | 21 | 15442 | ||
2 | 37 | 37 | 16351 | |||
3 | 33 | 33 | 17003 | |||
4 | 19 | 19 | 18116 | |||
5 | 31 | 31 | 18406 | |||
极值:五个最大值,五个最小值
正态性检验 | |||||||
性别 | Kolmogorov-Smirnova | Shapiro-Wilk | |||||
统计量 | df | Sig. | 统计量 | df | Sig. | ||
薪水 | 女 | .119 | 26 | .200* | .948 | 26 | .204 |
男 | .168 | 22 | .109 | .912 | 22 | .051 | |
*. 这是真实显著水平的下限。 | |||||||
a. Lilliefors 显著水平修正 | |||||||
从Sig的值大于0.05,说明男女员工的数据都是符合正态分布的,相反小于0.05不符合正态分布。
方差齐性检验 | |||||
Levene 统计量 | df1 | df2 | Sig. | ||
薪水 | 基于均值 | .073 | 1 | 46 | .788 |
基于中值 | .000 | 1 | 46 | .993 | |
基于中值和带有调整后的 df | .000 | 1 | 43.800 | .993 | |
基于修整均值 | .055 | 1 | 46 | .816 | |
Sig值都大于0.05,说明方差齐性,相反,小于0.05说明方差不齐性。
直方图
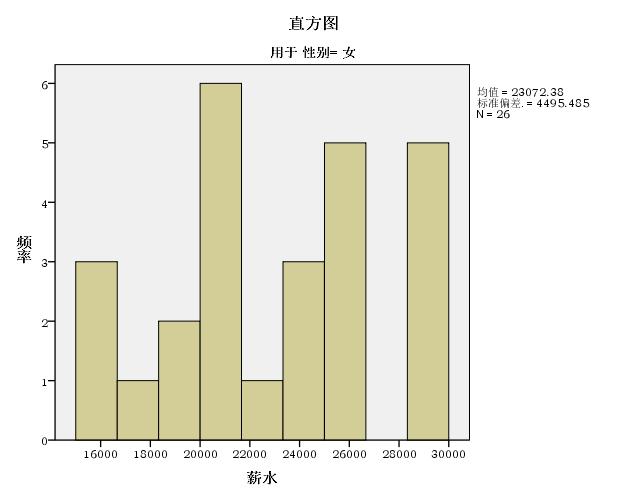
直方图——女
上图显示女性性别,直方图的正态分布不显著。
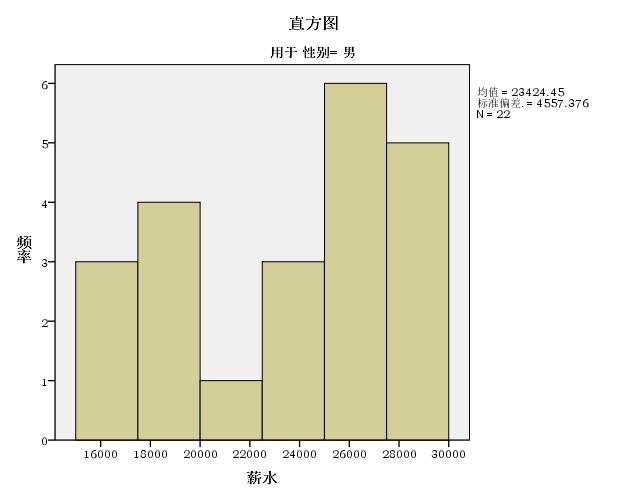
直方图——男
上图显示男性性别,直方图的正态分布也不显著。
茎叶图
薪水 Stem-and-Leaf Plot for
性别= 女
Frequency Stem & Leaf
3.00 1 . 555
.00 1 .
3.00 1 . 889
7.00 2 . 0011111
1.00 2 . 3
5.00 2 . 44555
2.00 2 . 66
5.00 2 . 89999
Stem width: 10000
Each leaf: 1 case(s)
例如:第一行,茎1加叶0.5,之后乘以10000
薪水 Stem-and-Leaf Plot for
性别= 男
Frequency Stem & Leaf
7.00 1 . 5678889
4.00 2 . 0334
11.00 2 . 55566677899
Stem width: 10000
Each leaf: 1 case(s)
正态 Q-Q 图
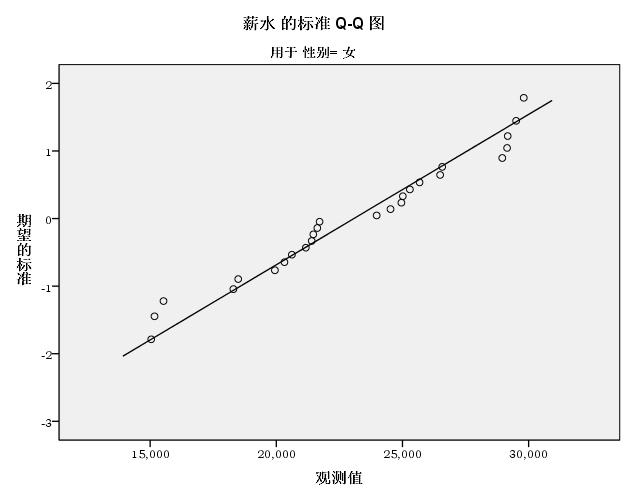
QQ图——女
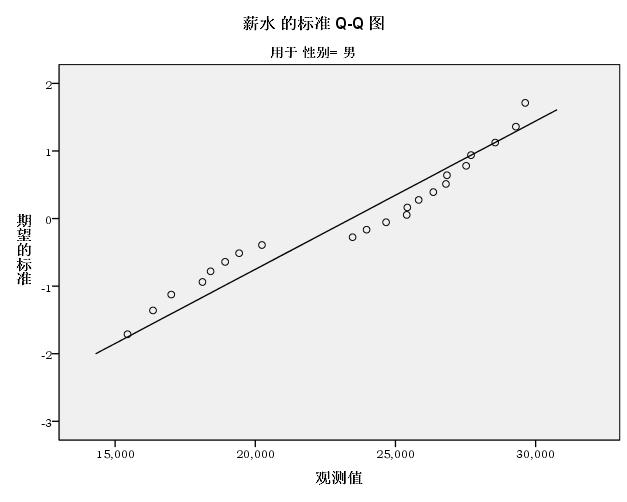
QQ图——男
图中斜线表示标准正态的线,其中的空心圈表示变量值,变量值越接近直线,表示数据越接近正态分布。
反趋势正态 Q-Q 图
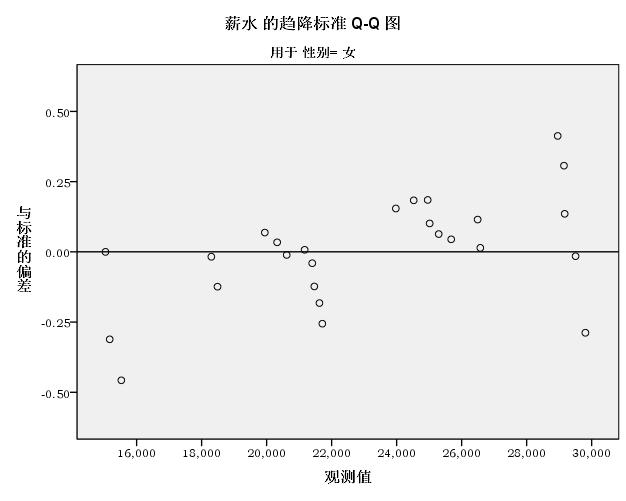
反趋势QQ图——女

反趋势QQ图——男
离散正态分布,变量的实际观测值作为横坐标,实际观测值与期望值的差作为纵坐标,若实际数据符合正态分布,表示图中的点分布在直线附近。
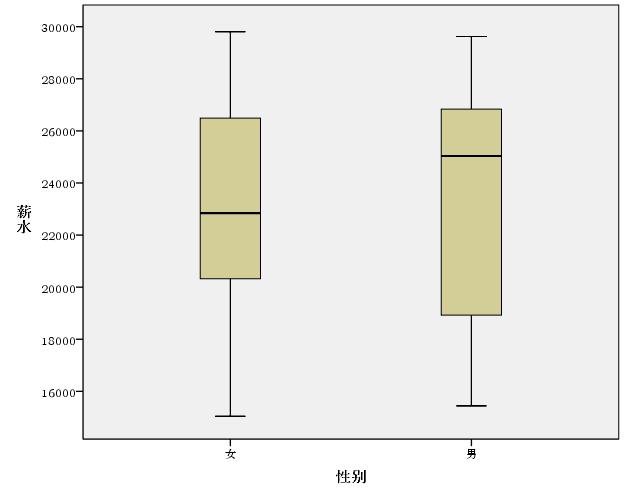
箱图
箱子的上边线代表的是75%的百分位数,下边线代表的是25%的百分位数,中间的是中位数,箱子的上横线和下横线表示除去离群值和极值以外的最大值和最小值,离群值是指距离箱子的上边和下边大于箱子高度的1.5倍到3倍之内的(圈),大于箱子高度的3倍以上的值(*)
分布水平图






